二元樹(Binary Tree)

樹 Tree

生活中常見各式各樣的數狀圖，像是族譜、賽程表等等，至於在計算機科學中，tree則是一種抽象資料型別(Abstract Data Type)，是一種具有階層式 (Hierarchical) 的數狀資料集合。

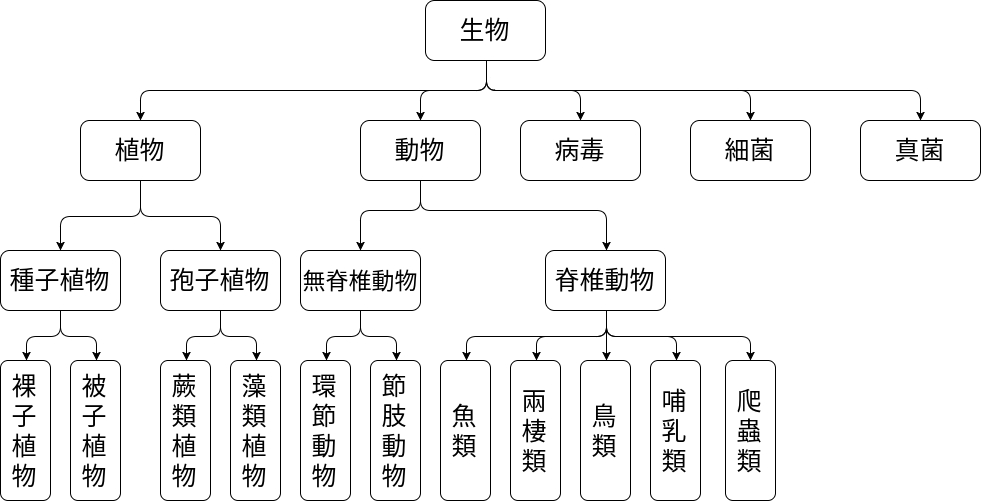
定義

樹 (tree) 是一個由一個或多個節點 (node) 所組成的集合，滿足以下兩點： 1. 有一個特別的節點叫作「根」(root) 2. 其餘的節點 (node) 可被分割為 n >= 0 個互斥 (disjoint) 的集合 T₁, ..., T_n , 每個集合都是一棵樹，並且稱作根的「子樹」 (subtree)

名詞介紹

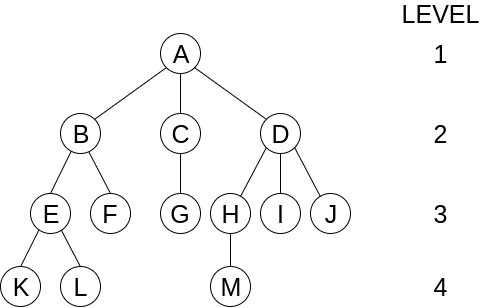
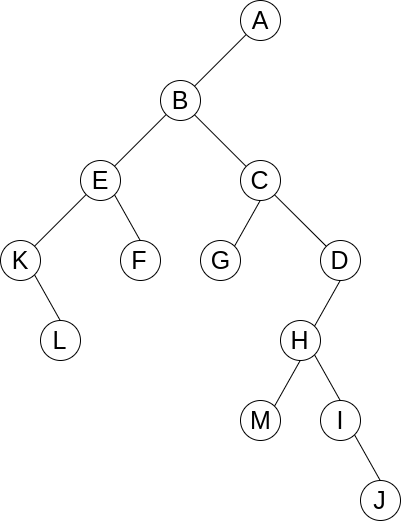
1. degree : 一個 node 子節點的個數，e.g. degree(A) = 3, degree(C) = 1, degree(F) = 0
2. leaf (terminal) : degree = 0 的 node，e.g. leaf = {K, L, F, G, M, I, J}
3. parent & children : A 是 B 的 parent, B 是 A 的 children
4. siblings : 具有相同 parent 的 nodes, e.g. B, C, D 是 siblings
5. degree of tree : 所有 node 的 degree 中最大值代表這棵數的 degree，degree 為 k 的樹又稱為 k-ary tree
6. ancestors : 一個 node 走回 root 所要經過的 nodes, e.g. M 的 ancestors 有 A, D, H
7. level : root 的 level 為 0 或 1，children 的 level 為 root 的 level + 1，以此類推
8. height (depth) : 所有 node 中 level 的最大值代表這棵數的 height (depth)

表示方法

1. List Representation

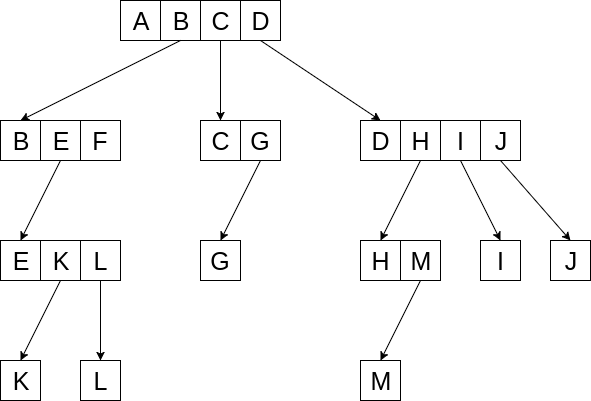
2. Left Child-Right Sibling Representation

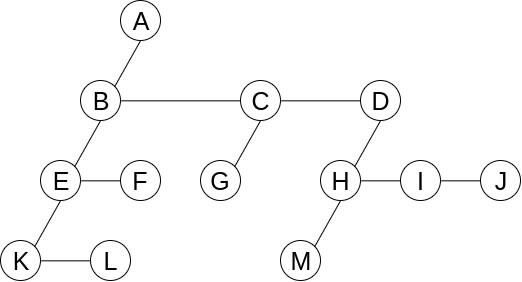
3. Representation as Degree-Two Tree (Left Child-Right Child)

二元樹 Binary Tree

以上介紹的tree並沒有限制subtree的數量，但我們一般較常用的還是接下來要介紹的二元樹 (Binary Tree) 。

二元樹有以下幾點特性： 1. 每個 node 的 degree 不超過 2 2. binary tree 可以不存在任何的節點 (empty) 3. 需要區分左子樹與右子樹，也就是左右子樹互換位置的話就會形成另一個新的樹

二元樹的表示方法

1. Array Representation

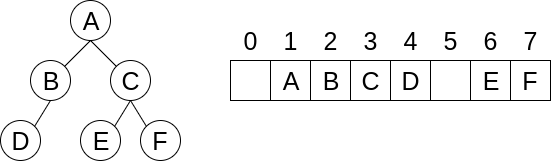
使用array來表示binary tree通常會具有以下的特性： * parent index = ⌊ current index / 2 ⌋ * leftChild index = current index * 2 * rightChild index = current index * 2 + 1 但是使用array表示，常常會造成空間上的浪費，如：

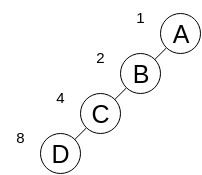
能夠最有效利用array空間的樹是complete binary tree，像是heap就非常適合用array進行實作。

2. Linked Representation

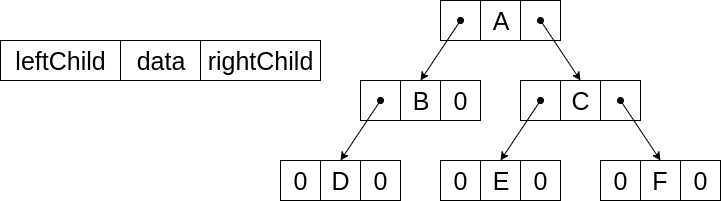
另一種表示方法是使用linked list實作，雖然每個node都需要額外的空間來儲存link，但是對於空間上的利用卻能夠進行比較有效的管控。

實作

以下使用python以Linked List實作Binary Tree。

首先定義樹的節點：

1
2
3
4
5

class TreeNode():
    def __init__(self, data=None, left=None, right=None):
        self.data = data
        self.left = left
        self.right = right

接著是二元樹的類別以及基本方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class BinaryTree():
    def __init__(self, root=None):
        self.root = root
    
    def isEmpty(self, node):
        return node is None

    def left_child(self, node):
        if self.isEmpty(node):
            return
        return node.left

    def right_child(self, node):
        if self.isEmpty(node):
            return
        return node.right

二元樹的遍歷 Traversal

若遍歷一棵樹具有以下三個步驟，
* L: moving left * V: visiting the node * R: moving right

則遍歷的方法就有，L,V,R 三種步驟的排列數 = 3! = 6 種: LVR, LRV, VLR, VRL, RLV, RVL 。

取其中三種當作遍歷的方法： * preorder:   VLR * inorder:       LVR * postorder: LRV

記的方法很簡單，看 V 的位置就對了，若 V 的位置在前面就是preorder，在中間就是inorder，在後面就是postorder。

1. Inorder Traversal
   

   1 2 3 4 5

   def inorder(self, node): if node: self.inorder(node.left) print(node.data, end=" ") self.inorder(node.right)

2. Preorder Traversal
   

   1 2 3 4 5

   def preorder(self, node): if node: print(node.data, end=" ") self.preorder(node.left) self.preorder(node.right)

3. Postorder Traversal
   

   1 2 3 4 5

   def postorder(self, node): if node: self.postorder(node.left) self.postorder(node.right) print(node.data, end=" ")

4. Level-Order Traversal
   第四種遍歷的方法，依照node的level的順序依序拜訪各結點。

1
2
3
4
5
6
7
8
9
10
11
12
13

def levelorder(self, node):
    if not node:
        return
    from collections import deque
    queue = deque()
    queue.append(node)
    while queue:
        node = queue.popleft()
        print(node.data, end=" ")
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)

其他操作

1. 複製

   1 2 3 4 5

   # Return a Pointer to a same data from original node def copy(self, node): if node: return TreeNode(node.data, self.copy(node.left), self.copy(node.right)) return None

2. 相等

   1 2 3 4

   @staticmethod def equal(first, second): return (not first and not second) or (first and second and (first.data == second.data) \ and BinaryTree.equal(first.left, second.left) and BinaryTree.equal(first.right, second.right))

(未完成，待補上...)